Upper sum
The upper sum of a function f on the interval [a,b] divided into n parts is the sum of the areas of n consecutive rectangles between a and b, all of which have a height equal to the maximum function value in the corresponding interval. One has to enter the left and right boundary value (that is a and b) of the range over which the upper sum has to be calculated, and also the number of intervals (n). The slider for the accuracy can now be used to change the accuracy of finding the maximum per interval. Here we see an example of the upper sum of 2*sin on the interval [0,pi] divided into 10 parts.
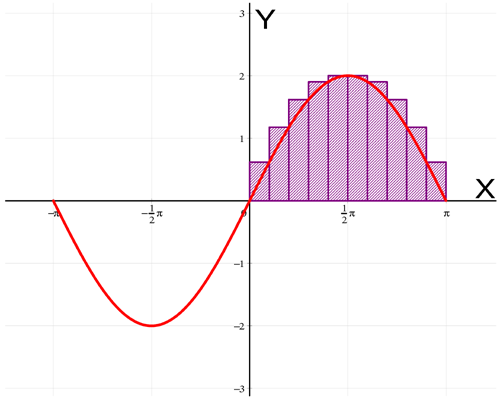
VisuMath shows that the upper sum is equal to 4.59537. We see that the value is bigger than the real area under 2*sin between 0 and pi . The upper sum approaches the area better when the number of subdivisions is increased, as can be seen in the following figure in which the number of intervals in increased to 20.
The upper sum is now equal to 4.30593.
Lower sum
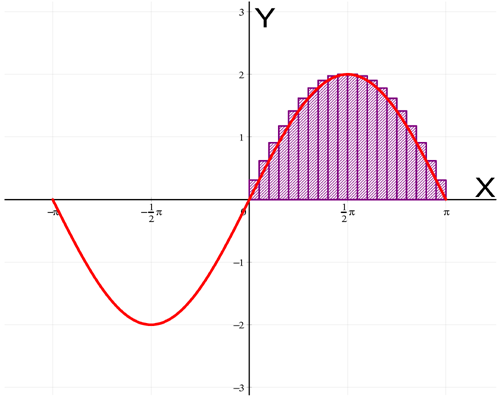
The lower sum of a function f on the interval [a,b] divided into n parts is the sum of the areas of n consecutive rectangles between a and b, all of which have a height equal to the minimum function value occurring in the corresponding interval. The left and right boundary values (a and b) of the range over which the lower sum has to be calculated, and also the number of intervals (n), must be entered. The slider for the accuracy can be used to change the accuracy of finding the minimum per interval. Here we see an example of the lower sum of 2*sin on the interval [0,pi] divided into 10 parts.
VisuMath shows that the lower sum is equal to 3.33873. Also the lower sum approaches the real area better when the number of subdivisions is increased. With 20 subdivisions we obtain the following situation:
The lower sum is equal to 3.67761.
Riemann sum
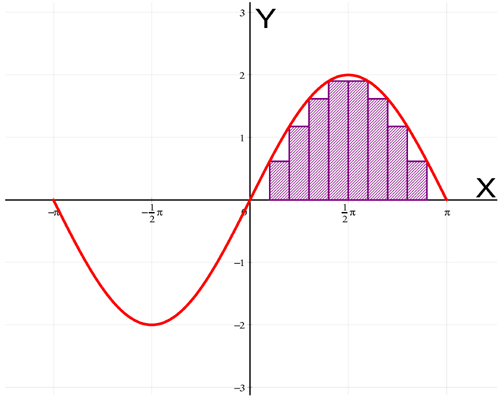
The Riemann sum of a function f on the interval [a,b] divided into n parts is the sum of the areas of n consecutive rectangles between a and b, all of which have a height equal to the function value in one of the points of the corresponding interval. Also here, one has to enter the left and right boundary values (a and b) of the range over which the Riemann sum has to be calculated, and the number of intervals (n). The slider for the accuracy can be used to change the accuracy of finding the function value per interval. A second slider can be used to position the point within the subinterval for which the program computes the function value. Is the slider located in the middle, then the middle point of each interval will be used. Sliding the slider to the left, resp. to the right, corresponds to sliding the point to the left, resp. right. Here we see an example of the Riemann sum of 2*sin on the interval [0,pi] divided into 10 parts, for which the middle points are used:
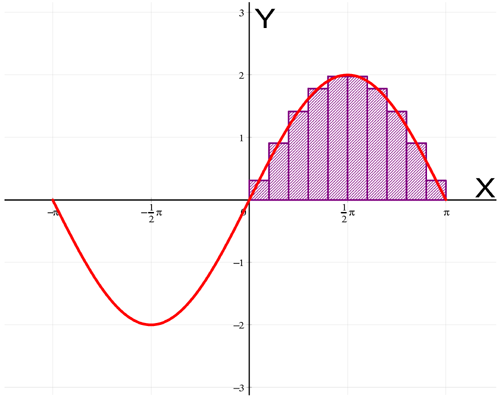
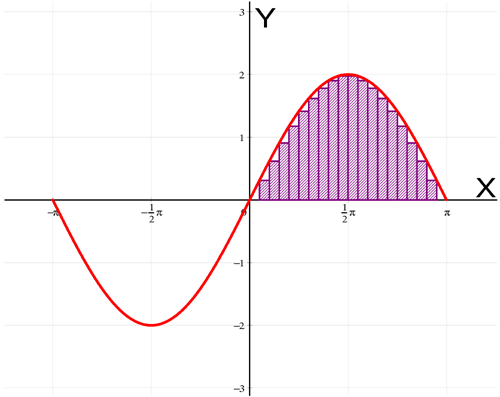
VisuMath returns that the Riemann sum is equal to 4.01650. Also the Riemann sum approaches the exact area better when the number of subdivisions is increased. With 20 subdivisions we obtain the following situation:
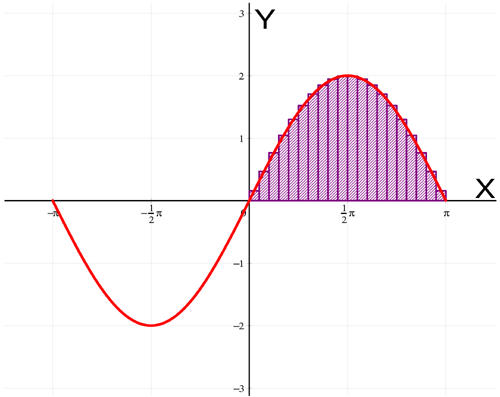
The Riemann sum is now equal to 4.00412.
Integral
The integral of the function f on the interval [a,b] is the exact (algebraic) area between the x-axis and the graph of f between a and b. We notice that the area is negative when the graph is beneath the x-axis. Here we see the area under the graph of 2*sin between 0 and pi.
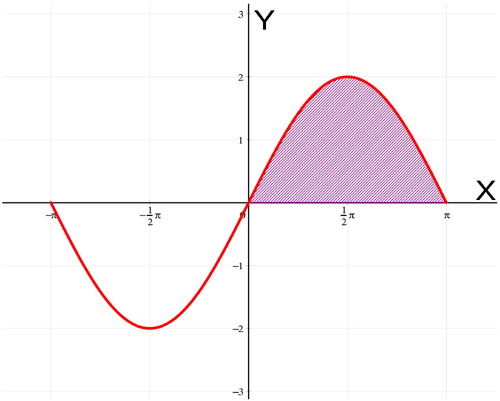
The area equals 4. VisuMath calculates this result numerically. We remark that the techniques used only give good results if the function to be integrated does not have any singularities on the given interval. So, it must be continuous on the whole interval.