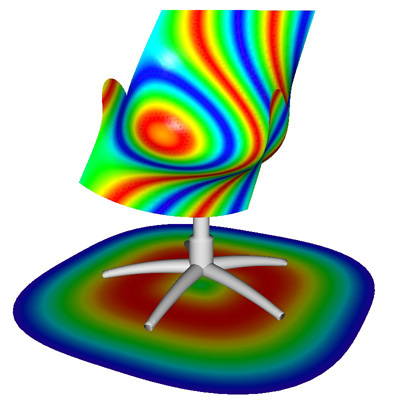
A mathematical office chair (OfficeChair.vim)
This example shows how it is possible to construct a rather complex model, including the carpet, with only four mathematical equations. Different types of equations are used for this. More precisely, the example makes use of a parameter equation, an implicit equation, cylindrical coordinates and a tube. The use of the frac function makes it possible to define the five legs of the chair with only one equation. By deselecting equation 4 and selecting equation 3 instead, the legs of the chair are replaced.
A Möbius type of surface situated in a torus (SolidMobiumStripInTorus.vim)
The Möbius strip as an example of a non orientable surface is wellknown. The surface you can see here is a torus constructed by rotating an ellipse along a vertical axis. During this process, however, the ellipse itself is also rotated along the line tangent to the rotation circle. In order to close up the surface nicely, the full rotation along the axis corresponds with a half rotation along the tangent line. The ellipses are made visible in the animation by means of the coloring of the surface. The torus obtained here is of course orientable, but if the semiminor or semimajor axis of the ellipse vanishes, then the Möbius strip is obtained.
This surface can fit nicely into a regular torus of revolution as can be seen in the model. In fact, this observation makes it possible to physically construct the "Solid Möbius strip" of wood, as the author's father in law Jozef Vantieghem actually did. You can find the result in the image below.
Moreover, the model in VisuMath is made "inflatable". This means that the semiminor axis is a parameter that can have several values. If one runs the animation, the surface is constantly inflated and deflated.
 |
 |
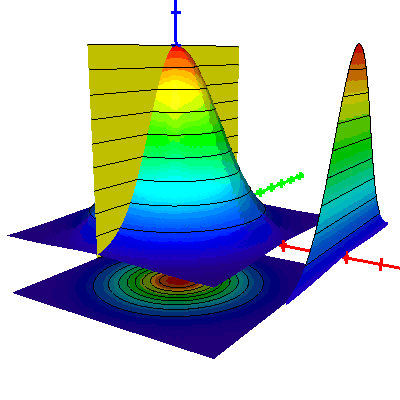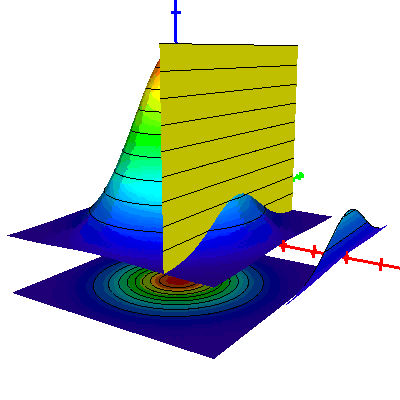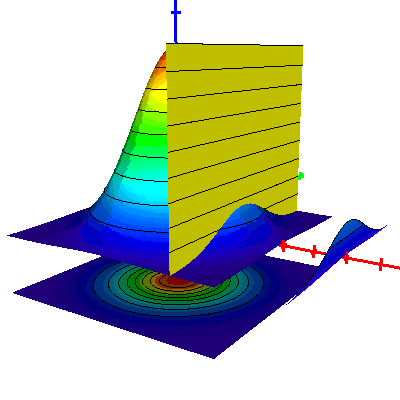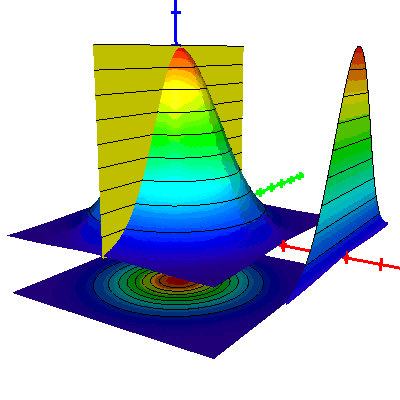
The bivariate normal distribution (BivariateNormalDistribution.vim)
This example demonstrates that the intersection of the surface determined by the bivariate normal distribution with a vertical plane gives rise to the univariate normal distribution. In the model, the color function is activated for some of the surfaces. Furthermore, the implemented animation shows a moving vertical plane and the projection of the intersection, as illustrated below. We remark that the quality of the gif animation shown here is inferior to the animation that can be viewed in VisuMath, because of the limited number of colors that can be used in gif files.
Observe in this model also the projection of the bivariate normal distribution onto the xy-plane. This illustrates that also projections can be realized with VisuMath.
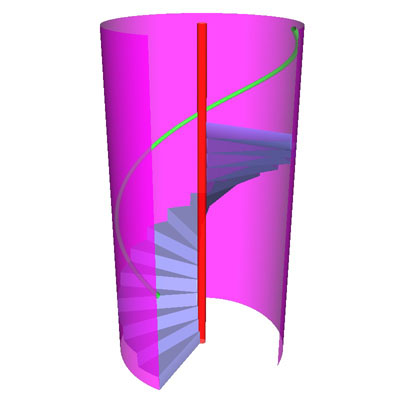
The spiral staircase (SpiralStaircase.vim)
This example shows how a spiral staircase can be modeled. Mathematically, the model is constructed from a helicoid, but is made discrete in order to simulate the different stairs. The handrail has the shape of a helix and is constructed by means of a tube around this helix. Interesting with this model is the use of parameters. Indeed, the three parameters a, b and c are set in the parameter section and have a specific meaning:
- a: represents the number of stairs;
- b: represents the distance between the bottom and top level;
- c: represents the radius of the cylinder in which to situate the staircase
A heart (Heart.vim)
This example shows a heart shaped surface determined by an algebraic implicit function, along with its three main projections. Level curves are visible as well. Moreover, by varying the parameter, the heart starts to beat, including all its projections. This example can be useful to find out how to project a surface onto a plane parallel to one of the coordinate planes.

An arbor (Arbor.vim)
This example demonstrates again that rather complex shapes can be modeled by means of a limited number of mathematical functions. The model shows an arbor that is a bit special in the sense that the top part can rotate as the animation illustrates.